Resolution of Capillary Chromatography

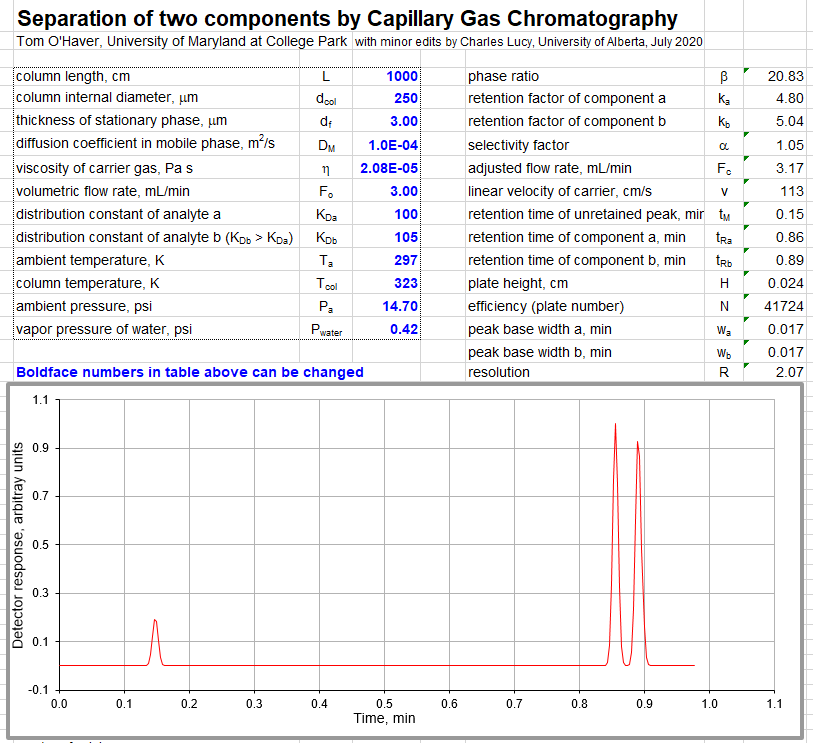
Shows how a difference between the distribution coefficient of two components can lead to separation in capillary gas chromatography. Students select column length, column internal diameter, thickness of stationary phase, diffusion coefficient in mobile phase, viscosity of carrier gas, flow rate, ambient temperature, and column temperature. The simulation calculates the phase ratio, selectivity, linear velocity of carrier, retention time of unretained peak, retention time of the two components, plate height, efficiency (plate count), peak base width, and resolution. Displays plot of simulated chromatogram showing two component peaks and an unretained peak.

Excel format: Capillary.xls (with improvements by Charles Lucy, University of Alberta, July 2020)
 

Inputs:
column length, cm	L	
column internal diameter, cm	id	
thickness of stationary phase, cm	df	
diffusion coefficient in mobile phase, cm2/min	Dm	
viscosity of carrier gas,  poise	eta	
volumetric flow rate, mL/min	Fo	
distribution coefficient of component a	Kda	
distribution coefficient of component b	Kdb	
ambient temperature, K	Ta	
column temperature, K	Tc	
ambient pressure, psi	Pa	
vapor pressure of water, psi	Pwater	

Outputs:
phase ratio	ß =i d/(4*df)
ka = Kda/beta
kb = Kdb/beta
selectivity	a = kb/ka
adjusted flow rate, mL/min	
  Fc = Fo*(Tc/Ta)*(Pa-Pwater)/Pa
linear velocity of carrier, cm/min	
  v = Fc/(3.14159*(id/2-df)^2)
retention time of unretained peak, min	to = L/v
retention time of component a, min   tra = (ka*to)+to
retention time of component b, min   trb =( kb*to)+to
plate height, cm	
h = (2*Dm)/v+((id/2)^2*((1+6*kb+11*kb*kb)/
  (24*(1+kb)*(1+kb)))/Dm)*v
efficiency (plate count)	N = L/h
peak base width a, min	twa = tra/sqrt(N/16)
peak base width b, min	twb = trb/sqrt(N/16)
resolution	
R = sqrt(N)*((alpha-1)/alpha)*(kb/(1+kb))/4