Resolution of Capillary Chromatography
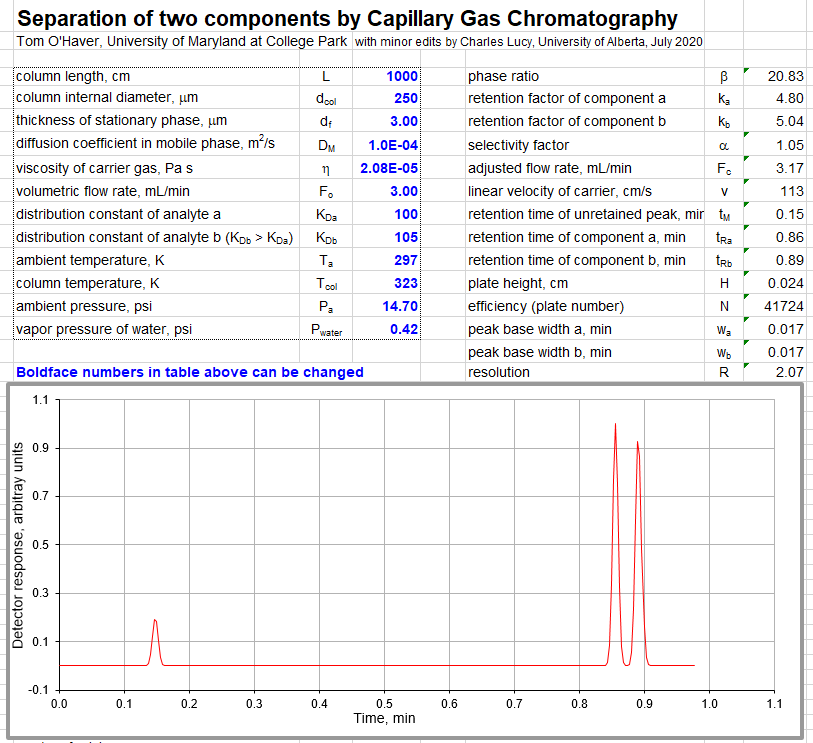
Shows how a difference between the distribution coefficient of two components can lead to separation in capillary gas chromatography. Students select column length, column internal diameter, thickness of stationary phase, diffusion coefficient in mobile phase, viscosity of carrier gas, flow rate, ambient temperature, and column temperature. The simulation calculates the phase ratio, capacity factor, selectivity, linear velocity of carrier, retention time of unretained peak, retention time of the two components, plate height, efficiency (plate count), peak base width, and resolution. Displays plot of simulated chromatogram showing two component peaks and an unretained peak.
Download links: Capillary.wkz;
Wingz player application and basic set of simulation modules, for
windows PCs or Macintosh
OpenOffice Calc format: Capillary.ods
Excel format: Capillary.xls
Inputs: column length, cm L column internal diameter, cm id thickness of stationary phase, cm df diffusion coefficient in mobile phase, cm2/min Dm viscosity of carrier gas, poise eta volumetric flow rate, mL/min Fo distribution coefficient of component a Kda distribution coefficient of component b Kdb ambient temperature, K Ta column temperature, K Tc ambient pressure, psi Pa vapor pressure of water, psi Pwater Outputs: phase ratio ß =i d/(4*df) capacity factor of component a ka = Kda/beta capacity factor of component b kb = Kdb/beta selectivity a = kb/ka adjusted flow rate, mL/min Fc = Fo*(Tc/Ta)*(Pa-Pwater)/Pa linear velocity of carrier, cm/min v = Fc/(3.14159*(id/2-df)^2) retention time of unretained peak, min to = L/v retention time of component a, min tra = (ka*to)+to retention time of component b, min trb =( kb*to)+to plate height, cm h = (2*Dm)/v+((id/2)^2*((1+6*kb+11*kb*kb)/(24*(1+kb)*(1+kb)))/Dm)*v efficiency (plate count) N = L/h peak base width a, min twa = tra/sqrt(N/16) peak base width b, min twb = trb/sqrt(N/16) resolution R = sqrt(N)*((alpha-1)/alpha)*(kb/(1+kb))/4