Chemistry on-line Conference, 1997. Paper 6.
Nature doesn't solve equations, so why should we?
Mathematically-lean simulations in chemistry
----
Hugh M. Cartwright
Physical and Theoretical Chemistry Laboratory,
Oxford University
South Parks Road, Oxford, England OX1 3QZ
hugh@muriel.pcl.ox.ac.uk
This paper is available with full-size graphics (this file), or
with graphics cut down slightly to make display easier on PCs
or macs with smaller screens. (ccpap6tn.html).
To enhance display speed, you may download this
paper by anonymous ftp from muriel.pcl.ox.ac.uk Retrieve all files
from the pub/papers/chemconf97 directory using binary mode,
then use a web browser to view ccpaper6.html. A Postscript version of the
paper is available in pub/papers
e-mail can be sent to the author by clicking on the e-mail address above.
1 Introduction
2 The place of simulation in the
undergraduate course
3 Categories of simulation
4 The advantages of simulation
5 Advantages of mathematically-lean simulation
6 Comment
1. Introduction
During the last decade the style of university chemistry teaching has
changed radically. Computers were once rarities, but are now
commonplace, and their use enhances many
courses. As universities compete to attract students from
a limited pool, the skill with which chemistry departments can
weave new technology into their courses is becoming an important
consideration for many candidates.
Computers are somewhat cheaper than most scientific instruments and
considerably cheaper than a professor. It is not surprising then that
they are in widespread use (Table 1).
|
Table 1.
Typical computer use in university chemistry departments.
 Provision of access to, and maintenance of, databases of scientific data or
student records
Provision of access to, and maintenance of, databases of scientific data or
student records
 Automation of exam setting and marking
Automation of exam setting and marking
 Provision of word processing and graphic design facilities for students
and staff
Provision of word processing and graphic design facilities for students
and staff
 Tuition and guidance of students in problem-solving
Tuition and guidance of students in problem-solving
 Numerical computation in areas such as
molecular dynamics
Numerical computation in areas such as
molecular dynamics
 Control of instruments and data acquisition
Control of instruments and data acquisition
 Analysis of data using spreadsheets or mathematical packages
Analysis of data using spreadsheets or mathematical packages
 Control and display of simulations
Control and display of simulations
|
|---|
The contribution which computers make varies from one department to another,
depending on the machines available, local expertise, and the teaching
philosophy of the department. Consequently, their impact on student
learning is far from uniform.
Where the computer is used primarily as
an administrative tool, for example to store student records,
there is little direct benefit to the student. Similarly, when
students have ready access, but the
computer is
used just to word process laboratory reports or assignments, it does not
contribute a great deal to scientific understanding. Students' keyboard
and computer skills improve, but the computer is not helping
them to understand "why things are the way they are".
Even when employed scientifically, if computers are used to help students to balance equations or follow
VSEPR rules, the software may just be a disguised
"programmed learning" text. The application of rules to determine
molecular shapes or balance equations is, in a sense, a mechanical
operation which can be carried out without knowledge of the underlying science.
The primary aim of a chemistry
course must be to develop in students an appreciation of how the
material world behaves, and this requires that the computer
play an active, positive role in learning.
The key to this is the simulation. Simulations
have long been a part of chemistry, and although longevity
is not in itself a
persuasive argument for their use, they find a place in most courses. We argue in this paper that
one of the most valuable uses of the computer in a chemistry course is to run simulations
which develop understanding of the molecular world.
Detailed simulations of scientific phenomena
can provide an
insight which transcends a mathematical description,
and an understanding of how materials behave is at least as
important as being able to express that behaviour in algebraic
terms. By interacting with a computer model students can develop
an understanding that - at its best - becomes almost intuitive.
At the most fundamental level, a simulation visualises the
- possibly idealised - behaviour of individual atoms and molecules.
The level of detail may be limited by the facilities available,
(it is a common observation that, no matter how much computer power is available to
a chemist, it is never enough).
Nevertheless, sophisticated simulation is not always necessary; a
detailed view might conceal important generalisations,
and thus be counterproductive. Consequently, both
molecular level simulations and their coarser counterparts,
in which behaviour in the bulk is simulated, have a
role to play in a chemistry course. It is important to realise, though,
that they are not equivalent. Visualisation of
equations, which is essentially what most bulk-level
simulations involve, is one step removed from the "real" world of atoms and
molecules; we shall argue that in some ways this lessens their value and their
impact in teaching.
Computer visualisation can be introduced almost anywhere in a
chemistry course, but grapeshot firing of simulation into it
is rarely desirable. A simulation must justify its place no less
rigorously than a lecture or practical experiment. (Equally,
lectures and experiments should be able to justify their
existence against the competition provided by simulations).
To do this, the simulation must teach concepts more
efficiently, or give students a special insight into a topic,
or perhaps
link together disparate areas of the subject. It must not be a
soft financial option whose raison d'etre is to allow
administration to replace professors, or keep students quiet
when there are not enough spectrometers to go around.
Variety is
beneficial in learning, so a mixed diet of
simulation, lecture, experiment and discussion will do much to
stimulate students' appetite for chemistry.
Simulation is a broad field, and much variety exists, limited primarily by
the inventiveness of those who write the software. Most simulations can be
placed into one of the following categories:
3.1 The Black Box Simulation
In a Black Box Simulation the computer mimics some of the behaviour of a
real or imaginary instrument (Fig 1). A complete virtual instrument
may be available, or
even a
virtual laboratory [10]
; in other cases users may select discrete components from a Grey Box
and bolt them together to make
their own Black Box. In this way they might, for example,
construct an
electrical circuit from standard items such as resistors and capacitors.
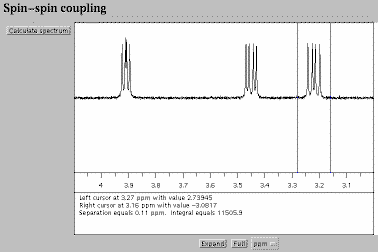
Fig. 1. The spectrum calculated by a "Black Box" NMR instrument.
This display is created by a Java
applet [1]. Full size version of this figure.
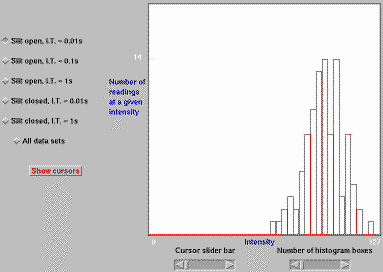
Fig. 2. Data from an on-line optical rig, gathered remotely
and displayed using Java applets [2]. Full size version of this figure.
Most of the earliest simulations in chemistry were built around the
interpretation of equations describing bulk behaviour. For example,
the P-V-T behaviour of an ideal gas can be understood by investigating
how the volume of a gas trapped by a moveable piston changes as the
pressure or temperature of the gas is adjusted. Such a
simulation is independent of the behaviour of individual molecules.
Indeed, even the presence of molecules is not acknowledged, since it
is the behaviour of an equation which is simulated (in this case,
PV=nRT ), rather than the behaviour of an aggregation of
molecules.
While this paper argues that simulation of equations is not always
the most productive way to proceed, sometimes such an approach is unavoidable. Fig 3 illustrates
a simulation of the Belousov reaction, in which calculation
at the molecular level is very involved, so that
bulk calculation is the only realistic way to proceed.
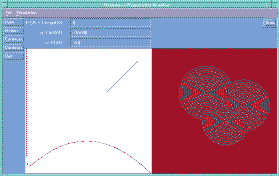
Fig 3. The development of concentric rings of concentration
minima in the Belousov reaction [3]. Full size version of this figure.
3.3 Visualisation of idealised behaviour
Simulations need not be correct to be useful. From the Bohr
planetary model onwards, students meet chemical models which are
idealisations or approximations. On occasion it is
helpful to isolate for inspection one aspect of molecular behaviour
which, in a real
system, cannot actually be isolated.
Molecular vibration provides an example. Even molecules of modest size
have many modes of vibration (according to the 3n-5 rule for linear
molecules, or 3n-6 for non-linear molecules, where n is the number
of atoms in the molecule). The vibrational motion which results
is complex, even in quite simple molecules (Fig. 4).

Fig. 4. A vibrating molecule displayed by a Java applet. [4] Full size version of this figure.
In any molecule all vibrations are active (though not usually excited) at
room temperature, because of zero-point energy. A scientifically
accurate depiction of a vibrating molecule shows all
atoms moving in what appears to be chaotic motion.
The amplitudes
of vibration are small (of the order a few percent of the equilibrium bond
lengths). The combination of these small amplitudes with the many
simultaneous vibrations makes it impossible
to divorce the vibration of a single segment
of the molecule from vibrations of the whole.
When students meet normal modes and characteristic
frequencies, it is helpful to discuss the vibrations of
functional groups as though a group were capable of vibrating
in isolation from the rest of the molecule.
This can be illustrated using an idealised model in which only one mode is
active. This qualitative picture - though
unrealistic - both clarifies the concept of characteristic
functional group frequencies, and can be used to show how
one specific vibration affects the symmetry of the molecule, thus leading
into selection rules. What is essentially a scientifically unjustifiable
simulation can in this way be of value.
Simulations at the molecular level - that is, those in which each
molecule in the simulation is treated individually - encapsulate all
simulations which describe the behaviour of material in bulk,
since bulk behaviour is the aggregation of the behaviour of the
constituent particles.
Such simulations are computationally
demanding, and represent the practical limit of simulations at
present, since a further dissection into the movement of electrons
and nuclei leads to intractable calculations.
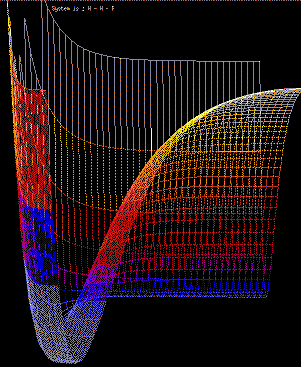
As an example of such a simulation, Fig 5 shows the establishment of a concentration
gradient for argon atoms above a solid surface
under the influence of (very strong!) gravity.

Fig. 5. Simulation of the movement of gas phase argon atoms
above a solid
surface. [5] Full size version of this figure.
In this simulation every atom (both in gas phase and solid phase)
is treated individually, and no "bulk" equations are used.
There are various advantages to such a simulation, which we
shall shortly consider. We can note immediately that
minimal assumptions are made in the calculation: we assume
only that
 collisions are elastic
and that
collisions are elastic
and that
 energy is a function of vertical
position.
energy is a function of vertical
position.
Complex behaviour (such as
the Maxwell-Boltzmann distribution of molecular speeds, or the
Boltzmann variation of density with height) emerges readily from the
simulation, and it is the way in which detailed physical
behaviour can be shown to be the result of simple physical interactions that represents
one of the most potent features of molecular-level simulation
A simulation is of course just one way of allowing students
to use computers to understand science. However, simulations in general have a number
of special advantages.
Among the most noteworthy advantage is that
simulations can generate images of considerable power (Figs. 6 and 7).
Such images can help students remember details in a way which equations cannot.
(Many of us will remember some striking simulation or
visualisation, but - to take an example at random - were any of us struck at first sight by the form of the van't Hoff
Isochore? ).
Interactivity is also a powerful argument in favour of simulation.
Users quickly become bored if they are just
passive consumers of information. They learn better
when they need to respond frequently to,
and have control over computer software.
It should be appreciated, though, that interactivity carries with it some dangers.
A conventional program which channels
all users along a pre-defined track depends on that track
being chosen with care, and on it being suitable for almost every user.
Interactive software by contrast presents the user
with many facilities and numerous choices. This flexibility
may remove from the user
any sense of direction, so that they become lost
within the software package.
The academic objectives of the
work may become unclear, and the user may wander inefficiently through
attractive but meaningless exercises. Interactive software must therefore be sufficiently structured
that users do not lose sight of the educational target.
The use of html wrappers and embedded Java applets
can provide this essential structure, though there are
of course other equally effective ways of ensuring that users are
not submerged in a complex, multi-faceted simulation.
In any set of computer-mediated exercises the instructor must
decide upon the most suitable order in which topics are
to be presented. In mathematically-based or rule-based exercises a progression
from mathematical simplicity to sophistication may
be used.
Exercises might progress from point masses to
masses of finite volume and eventually to molecules.
This may be a justifiable course, but there is no
reason why an order determined
by an increase in mathematical complexity should coincide
with the order which is academically most desirable.
It might instead be desirable to
present a comprehensive simulation initially, and gradually uncover its
mathematical basis as the underlying science is studied.
Other, more controversial, arguments also exist in favour of simulation.
Women are under-represented in most areas of science, particularly
in the physical sciences. For many people who teach at school,
college or university, this is a cause of concern, and much
effort has been devoted to searching for ways to increase
the number of women in science.
The limited number of female science teachers and professors,
and the rarity of female scientists on the television may have an effect,
but there are probably other factors at work.
Anecdotal evidence - drawn from observation of a group of
students at Oxford - suggests that female
students are often harder working than male students, but may have less "flair" for science at
the university level.
By contrast, their male
compatriots sometimes seem to have a greater sense of scientific "intuition".
What does this mean? Suppose that, during a walk in the country or on a beach, we come across
a stream blocked by a child's dam. We can assess
whether it is a "good" dam (in the sense of being strong enough to hold the
water back) without considering any hydrostatic or
hydrodynamic equations. Indeed,
the problem of whether a particular sticks, stones and mud dam is "good"
would present a testing computational problem.
But how then do we assess the quality of the dam, if not by
using equations? Presumably, through
having built dams - or having seen them built - and
in so doing, having gained practical experience of what
a "good" dam looks like. We have accumulated a fund of
knowledge which is ill-defined, incomplete and fuzzy,
yet still useful scientifically. This is not "intuitive" knowledge
in the normal sense, but a collection of experience which gives
us a feel for how things behave.
Those students who possess this sort of scientific intuition have
built this up from childhood, perhaps through building dams,
throwing stones and falling off trees, but also - crucially - through the
challenge provided by science teachers whose approach is first
to get their students to understand the physical principles
of science, and only later to learn the rules, facts and
equations.
Scientific intuition
may help when students have to evolve appropriate
ways to tackle a novel problem, or rationalise a
newly-discovered equation, trying to understand why it
has some particular form. Inasmuch as simulations allow the user
to experiment and interact with the material world, they will
stimulate the development of this intuition. Simulations thus teach not only
a single topic, but provide also broader scientific
experience.
Much science depends upon the interpretation and use of equations.
Simulations of equations have a role to play, but the understanding
which students
gain from them is different from that which they derive from
molecular simulations.
Of course, all simulations make use of equations and rules. Without
a prescription to determine how objects appear on the computer
screen and interact with each other, there could be no simulation.
In a mathematically-lean simulation, these
equations and rules are kept to a minimum.
For example, returning to PV=nRT , a molecular simulation of gases
requires us only to assume that gas molecules move, that they do not
interact except during collisions, and
that collisions are elastic (no energy loss). If we
wish to introduce non-ideality, we can allow the molecules
to have non-zero size, or interact with a Morse or a
6-12 potential. Notice that our assumptions are physically
based. That is, we are assuming properties of the
components which make up the physical system, not assuming
equations which describe observed behaviour, such as the van der Waals
equation. This is the key idea behind mathematically-lean
simulations.
We have noted in section 3.4 that, from simple assumptions,
complex behaviour can be derived. We
now consider some further advantages of molecular-level simulation.
Equations exist which accurately describe a huge range of phenomena.
Science attempts to identify those aspects of
the natural world which behave in a predictable fashion, and to
rationalise them by constructing equations which describe that behaviour.
Although these global equations encapsulate the behaviour of the system
which they describe, it may be hard for students to extract from
them that detailed behaviour.
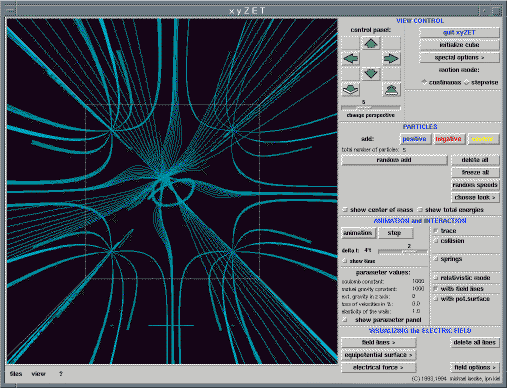
Let us consider an example from mechanics. Fig 8
shows a beam, hinged at its base, falling under gravity.
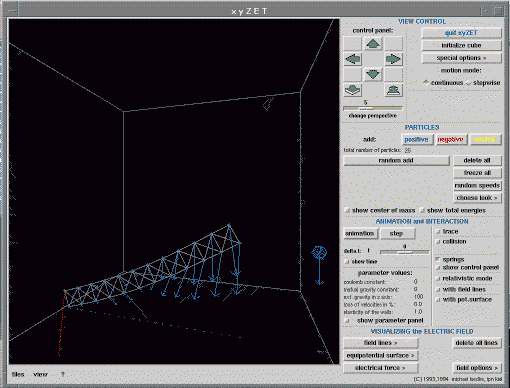
Fig. 8. A frictionless hinged beam falling under gravity. [6] Full size version of this figure.
Simulations whose role is to display the behaviour of equations usually
allow the user to specify only the values of parameters which
appear in the equation. There is
little point in allowing the user to set other parameters,
which do not affect the calculation.
In a molecular-level calculation, the few equations which underlie the
calculation are usually hidden from the user, and often
contain "within them" further equations (section 5.3). The user can then be permitted to vary a wide
range of parameters to investigate whether or not they influence
the system.
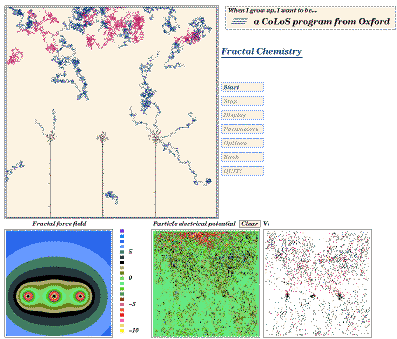
For example, the screen shot in Fig 10 is taken from a CoLoS
demonstration program dealing with fractal growth in solution.
It shows the semi-random motion of copper ions in a solution in
which three electrodes at an equal potential have been placed.
The user can investigate how the rate of growth and the form of copper fractals
depends upon temperature, solution viscosity, concentration,
potential difference and other factors. By making minimal
assumptions, but providing maximum flexibility, it is possible to
investigate combinations of parameters which the software
designer might never have considered. By calculating the
movement and interaction of ions at the most basic level,
rather than using equations which describe fractal deposition
directly, the user has considerable freedom to discover how
fractal growth is influenced by the various parameters.
A strong mathematical background is an asset to an
honours chemist. Nevertheless, many students find the language of mathematics difficult
or obscure. Simulations provide a means by which the mathematics can be made less
intimidating and the chemistry more palatable and understandable.
Students can, for example, learn qualitatively about the relationships between the
temperature of an assembly of molecules and the vapour pressure without
first (or ever!) meeting the Clausius-Clapeyron equation. They can
develop an understanding of heat capacity, or colligative
properties, from simulations such as that shown in Fig 11.

The Clausius-Clapeyron equation expresses the dependence of vapour pressure of a volatile solid
or liquid on temperature. It contains differentials (or logs in the
integrated form). It is an important
equation in thermodynamics, but though it is not
particularly complex, it still presents students with difficulties, and they
may not appreciate that vapour pressure rises approximately
exponentially with temperature. A simulation of a collection of molecules,
assuming a simple interaction potential, will
allow students quickly to investigate the dependence of
vapour pressure on temperature.
The experimental behaviour
is not "built-into" the simulation - indeed thermodynamic properties are
defined only for bulk systems, and the simulation is of
individual molecules. Nevertheless, with a sufficiently large
number of molecules, the user can measure vapour pressure and
investigate P/T relationships.
In a two phase (gas/solid) system, one can illustrate the
principles of Langmuir or BET behaviour using again simple interaction
potentials. (Fig 12).
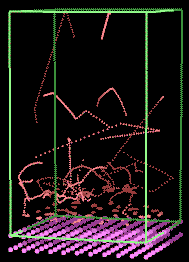
Fig. 12 Simulation of argon above a charcoal surface. The
movement of the argon atoms is illustrated by the tracks. [5].
Full size version of this figure.
This leads us to a further point of crucial importance:- molecular
simulations also simulate what we do not see.
This sounds like nonsense. What can it mean? Although the primary role of the simulation
shown in Fig 12 might be to allow students to study adsorption on solids, further physical phenomena may
be investigated using the same model. For example, the molecular tracks
in Fig 12 hint that the molecules adsorbed on the surface are
not actually stationary, but
move around a little. This behaviour is not "what we are looking for" if we
are using the simulation to
study Langmuir adsorption; indeed, this movement across the surface could not be observed if the simulation
was based solely on the Langmuir equation. In this sense then, the molecular
level simulation may include within it behaviour we are not looking
for (and may not even notice). The sudden discovery by a student of quite unexpected
phenomena, such as movement of adsorbed molecules, is both a stimulant
to learning, and often a source of delight to the student.
Let us return to the ideal gas law.
A simulation whose function was to allow students to understand the
behaviour of ideal gases could be visualised either at the molecular
level,
or through direct interpretation of the ideal gas equation.
Most students
need to memorise and be able to regurgitate equations in an exam.
But they need also to appreciate the physical origin of gas pressure,
that is, the bombardment of the walls of a
container by molecules. There is more fundamental understanding
to be gained by realising that, if the volume is restricted
the number of collisions of molecules with the walls
per second must increase, than by simply learning
that P depends inversely on V.

Fig. 13 A simple simulation of gas molecules confined to a small
container. [9]. Full size version of this figure.
5.5 Revelation of complex behaviour from simple equations
It is clear that complex behaviour can often
result from simple equations. The growth of fractals in solution, for example, can be
simulated using a random walk model in which ions in solution are
attracted to, and deposited on an electrode.
With the simplest of equations, quite complex behaviour can be modelled.
Fig 14 shows the symmetrical fractal obtained when a centro-symmetric
field is provided by an electrode in a dilute solution.

Fig. 14. Fractal growth resulting from a small centro-symmetric
field applied to an electrode in a dilute solution of copper ions [7].
Full size version of this figure.
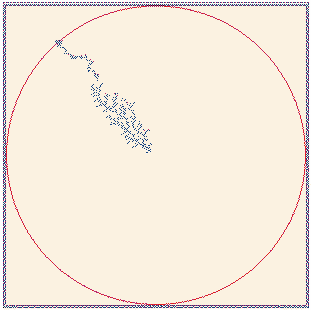
Fig. 15. Fractal growth by deposition of ions released
from a point source. Full size version of this figure.

Fig. 16. A fractal growth generated by an electrode which
provides a field aligned along the x-y axes. Full size version of this figure.
It would be unreasonable to expect simulation to sweep away the need
for students to be able to understand and use equations.
However, an appreciation of the physical world, promoted by
interactive simulations, can lay the basis for a deeper
knowledge of the raft of equations which chemists must know.
A chemist who understands only equations is really a mathematician.
A chemist who has a feel for the way in which molecules behave,
and who thinks that he or she knows what molecules want
to do is a scientist.
Appendix A: The CoLoS group
Several of the screen shots in this paper are from work by
members of CoLoS. CoLoS brings together scientists from many disciplines in
a variety of different countries, who share an interest in the effective use of
the computer in understanding science.
Readers who share this interest may like to know that CoLoS is offering
prizes for innovative scientific software available through the Internet.
First prize is one thousand dollars, travel from anywhere in the world
to a CoLoS conference, and day-to-day expenses for attendance at the conference.
The closing date for applications is expected to be February 1st 1998.
-
Further details
of the prizes.
-
Further details of CoLoS.
References and background information.
1. Taken from an
experiment in NMR spectroscopy
under
development in the Physical and Theoretical Chemistry Laboratory at Oxford University.
2. Taken from an on-line experiment in error analysis
under
development in the Physical and Theoretical Chemistry Laboratory at Oxford University. Data are generated by
connecting to
an optical rig through the Internet.
3. Data from Computer simulation of the Belousov-Zhabotinsky reaction,
Chi Ho Lam, Chemistry Part II thesis, Oxford, 1996
4. A
java applet
showing a vibrating molecule: http://www.pc.chemie.th-darmstadt.de/java/
5. Screen shot from a simulation written using X, C and Motif.
Pete Bennett, Mathematical modelling and computer simulation of aspects
of surface science, Chemistry Part II thesis, Oxford University, date.
6. An experiment under the control of the
CoLoS
program
xyzet,
developed at Kiel University, Germany.
7. Screen shot from an experimental
CoLoS
program on fractal growth, developed at Oxford University.
8. A screen shot from a
CoLoS
demonstration program on the thermodynamics of simple liquids. Andy Armstrong,
Computational modelling and simulation of molecular phase dynamics.
Chemistry Part II thesis,
Oxford University, June 1995.
9. A screen shot for a simple simulation of gas-phase molecules.
10. The virtual lab in Oxford is at
http://neon.chemistry.ox.ac.uk
11. An interactive computer simulation of collisional potential surfaces,
Russell Strevens, Chemistry Part II thesis, Oxford University, England, 1995
 Provision of access to, and maintenance of, databases of scientific data or
student records
Provision of access to, and maintenance of, databases of scientific data or
student records




 collisions are elastic
and that
collisions are elastic
and that



 Fig 9a. The initial configuration of the beam. Full size version of this figure.
Fig 9a. The initial configuration of the beam. Full size version of this figure.









